日能研、合格力実践テスト：算数（ゲーム）

日能研のコイン問題

日能研の合格力実践テスト，算数で出ていた２人でコインを取っていき，最後に取った人が負け，というゲームを題材とした問題。

子どもも一度はやったことがあると思います。

受験でもちょっとしたゲームを題材とした問題はよく出るため，実際の指導を元にちょっとお話したいと思います。

コインが何枚かあります。Ａ君とＢ君の２人が交互にコインを取り，最後に取った人が負けというゲームをします。１回に取れる枚数は２人とも１，２，３枚をどれか自由に選べます。Ａ君が先に取るものとして，次の問いに答えなさい。

（１）コインが６枚の時，Ａ君が必ず勝つためには，Ａ君は１回目に何枚取ればよいか。

（２）コインが１２３枚あるとして，Ａ君が最初に１枚取ったら，Ｂ君が必ず勝つためには，Ｂ君はこの次に何枚取ればよいか。

（３）Ａ君が１回目に３枚取ったとき，Ｂ君が必ず勝つためには，Ｂ君はその次に何枚取ればいいか。

答え：
（１）１枚
（２）１枚
（３）３枚

こういうゲーム系のものは，実際に試しながら負けないルールを見つけていくのがポイント。

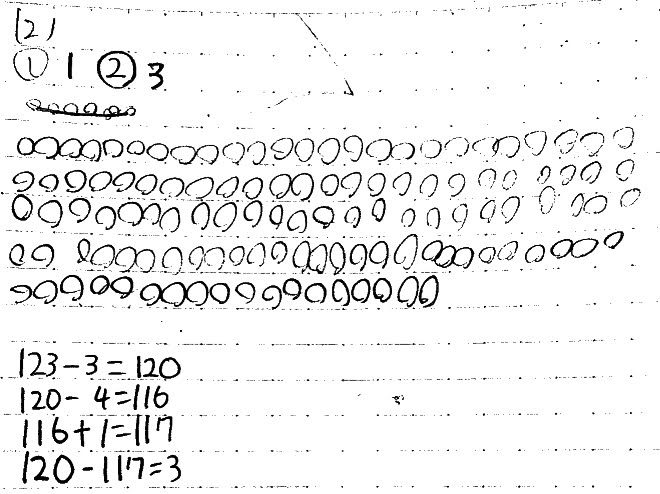
さすがに全部書き出して解くのはやりすぎ(^^;

しかし実際にやってみればわかる！という確信があって書き出したのは立派。

気付くために必要なのは，数を少しずつ増やして試すこと。

例えば（１）では６枚スタートでＡ君が必ず勝つには何枚取ればいいか，という問題。

これは最後に５枚残すように取ればいいというのはすぐにわかると思います。

よくわからなければ，〇を６個書いて試してみて下さい。

Ａ君が１枚取った時に，Ｂ君が何枚取っても勝てないとわかるはずです。※自滅は不可。

次に７枚スタートならＡ君は何枚取ればいいかを考えます。

この場合，先程と同じように残せば勝てるので，２枚取ればいいことになります。

８枚スタートでも同様にＡ君が３枚取ればいいことになります。

そして問題は次。

９枚スタートの場合は？

実際にやらせてみれば気付くと思いますが，９枚スタートではどう頑張ってもＡ君は勝てないのです。

なぜならＢ君が次のターンで確実に５枚残してしまうからです。

もしここまでで気付けなければさらに１０枚スタート，１１枚スタート，１２枚スタートと続けます。

すると１３枚スタートの時もＡ君に勝ち目がないことがわかります。

これをいくつかやれば，「４の倍数＋５」の枚数を残した段階で，既に勝敗が決していることに気付くはず。

もし気付かなければ，これに気付くようにアプローチ。

ＰＨＩの子の場合は１０枚くらい書き並べたところですぐに気づいたので，気付いた後は（２）（３）をササっと解けてしまいました。

このように規則の問題には必ず規則が存在します。

何を当たり前のことを言っているんだと思うかも知れませんが，絶対に存在するとわかっているこの規則に気付けないから解けないのです。

つまり，規則を見つける力を養ってあげれば，基本的にはどんな問題でも解ける，ということになります。

この１問をどう解くかではなく，この１問から規則の見つけ方を学ぶ。

これが１問の勉強から多くの問題を解けるようにするポイントです(^^)/