目次
円周率の美しさに涙する会
円周率への疑問を放置するのはもったいない!
毎年この疑問はよく耳にします。
しかしそれに対する親や先生の解答は決まっていて、

「そんなの覚えるものでしょ!小学生には求められないんだから考えるだけ時間の無駄。」
しかしそれはとても勿体ないことなんですね。
例えば、岩尾エマはるかさんは12歳で円周率に興味を持って以来、算数や数学に関する様々な影響を受け、2022年に円周率100兆桁を達成して世界記録を更新しています。
学校で円周率を習うのが小学5年生なので、12歳という年齢は決して早くもなく、むしろ塾に通っている子と比べると遅い方でしょう。
さらに岩尾さんは円周率に興味を持ったものの、算数、数学は苦手で、大学も文系に進学しています。
ところが大学で人間学から情報学へ変更し、コンピューターサイエンスを学び、そこから円周率で世界チャレンジに挑みます。
現在までにgoogleやパナソニックといった世界的企業で研究を行っています。
この経歴からもわかるように、算数や数学が苦手なことと、IT系を仕事にすることは、実は関係ないことがわかります。
文系、理系は、試験や科目として分ける都合上必要なものであり、本来ITだから数学ができなければいけない、なんてことはないのです。
むしろ大人の都合で分類したものが、子どもの先入観を与えることになっている可能性が大きいでしょう。
そして、些細な疑問を持つことが、将来に影響を及ぼすことも多々あります。
もちろん誰でも岩尾さんのようになれるとはいいませんし、岩尾さんには岩尾さんのめぐりあわせがあったのは事実でしょう。
しかしめぐりあわせを使えるのもまた重要なスキルであり、「文系だから無理」という思い込みでそのめぐりあわせをつかまなければ、この世界記録は達成できなかったはずです。
たかが円周率ですが、小学生なら誰でも疑問に思うことです。
「覚えなさい」と言ってしまうのは、そういう可能性の芽を摘んでしまうことになるので勿体ないですね。
実際、東大の入試でも円周率が3.05よりも大きいことを示せという問題が出されたのは有名ですね。
ということで、円周率に関する塾生の疑問を基に、どんなお話をしたのかまとめておきます。
もちろん受験には必要ないことばかりです。
しかし最近の入試では、思考力の一環として求められることがあり、さらに塾でも受験に出る関係から教えるところが出てきています。
でも、それも所詮受験のためなんですよね。
ファイではそれら受験のための要素は完全に廃して、子どもの興味のみに合わせて話しています。
また、内容も小学生が理解できる範囲のことにかいつまんでいるため、極力数式も用いません。
あくまで興味を持ってもらうことを目的としており、正確な知識を提供するものではありませんので、その辺はご留意下さい。
円周率とは
円周率は3.14や22/7で表される数で、円の直径に対する円周の割合となっています。
教科書でもそのように説明されており、一応それがイメージしやすい図も用意されていることが多いのですが、結局覚えていなければ計算できないということで、3.14という数字だけが独り歩きしがちです。
そのため、小学生は円周率を習った時に疑問に感じていることがあるものですが、その理由に対してのアプローチ方法を教えてくれる大人が周りにいないことが多く、放置されているのが現状です。
しかもゆとり教育全盛期には、円周率を3とする決定がなされているため、円周率が3ではないことを知らない大人もいる程です。
そんな状況なので、円周率を3,14に戻したところで、求められる人はほとんどいません。
しかし実際には原理さえ押させてしまえば、式自体は大したことないものが多く、やろうと思えば小学生でも円周率を求めることもできるのです。
ちなみに円周率は3.141592653589793238462643383279502…となっていますが、覚えることに意味はほとんどありません。
円周率の求め方
実際に測って円周率を求める
誰でもやってみることができる、一番簡単な確かめ方です。
円周=円の直径×π
なので、
π=円周÷円の直径
ということになります。
つまり、円周と直径をなるべく正確に測ることができれば、割ってみることで円周率を出せるということです。
ただ、これはどこまで正確に測れるかに左右されるので、実際にやってみると誤差も大きくなります。
しかしなるべく正確にやろうとすれば、3.0~3.2の間くらいには入る値を出すことができますので、試してみる価値は十分あるでしょう。
なお、この計算で出すことができるのは、普通の定規で長さを測った場合、10分の1まで読み取ることを考えると、0.1mmまでが有効数字ということになります。
cmで出すなら0.01cmまでですね。
つまりmmなら小数第2位以降の値は、計算上出たとしても無効な値ということです。
小学生ですと、計算で「3.141まで出た!」と言って競うことがよくあるのですが、普通の定規を使っている以上、どんなに頑張っても小数第三位以下は無効なのです(笑)
こういうときには誤差や有効数字の話をすると、また一つ学べますね。
正多角形の周の長さから円周率を求める
東大入試でも出題された円周率が3.05よりも大きいことを示すために用いられるのがこの方法です。
まず、直径が1の円にぴったりと入る正六角形を考えます。
直径を1にしたのは、円周率が直径に対する円周の長さの比率なので、直径が1なら円周の長さがそのまま円周率の値と同じということになるためです。
さて、この正六角形は円の中に入っているので、円周の長さよりも正六角形の周りの長さの方が短いことになります。
正六角形の1辺の長さは半径と同じ0.5になるため、周りの長さは3になります。
つまり、円周は3よりも長いことがわかります。
さらに正七角形、正八角形と角を増やして行えば、どんどん細かい値を出すことができます。
このように、多角形の角の数を無限に増やして円に近づけていくことができることから、円は正無限角形と解釈することもできます。
ちなみに東大入試の3.05より大きいことの証明は、正八角形で行えば出すことができますが、三平方の定理か三角比を用いないと実際に計算することはできないので、原理の理解にとどまります。
そしてこの方法を発展させ、球に内接する多角形と、外接する多角形を用いることにより、「内接する多角形より長いけど、外接する多角形より短い」と範囲を出すことができます。
これで正多角形の角を無限に増やし、範囲を絞り込んでいくことができるのです。
欧米で使われる22/7(7分の22)という円周率も、正九十六角形の中に内接する円を考えた場合、22/7(7分の22)よりも小さい数になることを証明できます。
正多角形の面積から円周率を求める(取りつくし法)
円の面積を出せれば円周も出せることになります。
そのことから、半径1の円を書き、その円に内接する正多角形と外接する正多角形の面積を求め、円の面積はその範囲内であるという方法で、円の面積を絞り込んでいくことができます。
例えば、円に内接する正六角形と外接する正六角形を書けば、円の面積はその2つの面積の間になることがわかります。
この正多角形の角の数を増やしていけば、徐々に円の面積に近づけていくことができます。
この方法は、アルキメデスにより行われ、取りつくし法といわれています。
この角を増やして計算していく方法は、無限に角を増やしていくことができるため、計算に終わりがありません。
ちなみにこの方法でアルキメデスは正九十六角形を用いて「円周率は223/71より大きくて、22/7より小さい」というところまで求めています。
確率から円周率を求める(ビュフォンの針)
レポート用紙のように、等間隔(間の距離がh)の線を用意し、その上に同じ長さ(長さℓ)の針を投げ落としていきます。
その結果、投げた本数に対して、何本の針が線にかかったかを数えます。
この時に出た確率は、2ℓ/πhとなることがわかっているので、
π=(2ℓ×投げた本数)/(h×線にかかった本数)
で円周率は求められることになります。
なぜこんな式で求められるのか、については、三角関数と積分を用いることになるので詳細は省きますが、簡単にイメージだけ話しておきます。
針が線にかかる確率は、針の中心と線との距離(x)、および針の角度(Θ)によって決まります。
よってこの2つの変数を基にした関数をつくると、条件がある範囲内に来ると、針が線と交わることがわかるグラフが作れます。
この部分の面積を全体の面積(積分で求める)で割ると、先ほどの式が出てくるというわけです。
円周率が関係してくる理由は、針の角度を要素として含んでいるからですね。
シミュレーションはこちら。
確率から円周率を求める(モンテカルロ法)
まず正方形を用意し、その中にぴったり内接する円を書きます。
そこにランダムに点を落としていくとき、円の内部に入る確率を求めると、それが円周率になるという方法です。
これはビュフォンの針と同じ原理なので、試行回数が多いほど、正確な値に近づいていきます。
なお、実際に確率から円周率にするときは、
点が円の中に入った回数/点を落とした回数=円の面積/正方形の面積
と考えられるので、円の半径をrとして求めると、
円の面積=πr2
正方形の面積=4r2
つまり円の中に点が落ちる確率はπ/4となるので、
円周率=確率×4
となることがわかります。
ちなみに、試行回数を10万回くらいやって始めて3.14まで出るようになるようです。
シミュレーションはこちらとこちら。
確率から円周率を求める(確率密度関数)
これを式で説明してしまうと小学生がついて来られないので、式での説明は省きます。
原理だけ説明すると、確率の分布は、試行回数を増やせば増やすほど、正規分布という山型の形に近づいていきます。
そしてこの分布は確率密度関数という式で求められる値と近似することがわかっています。
この確率密度関数の中に円周率πが含まれているため、実験では試行回数を増やして正規分布を求め、それを確率密度関数に当てはめて、方程式として円周率を求めることができます。
実際に試してみるなら、1/2(2分の1)の確率になるものが簡単なので、コイントスを用いて表と裏が出る確率の正規分布から円周率を求めるといいでしょう。
参考になりそうなサイト1,2,3。
無限級数を使って円周率を求める
同じ規則で足し算を繰り返していく式のことを、無限級数といいます。
例えば、
1+1/2+1/4+1/8+…と無限に足していくと、限りなく2に近づいた値を求めることができます。
このように、同じ規則で無限に足していって、求めたい値に近づけることができれば、足す数を増やしていくだけでどんどん答えに近づけていけることになります。
つまり、答えがπになる無限級数を求めれば、ひたすら足していくだけでどんどん答えが正確になる、ということです。
では答えがπになる無限級数などあるのか、ということですが、実は複数あることが確認されています。
その式の一つが1600年代に発見された
1/1ー1/3+1/5ー1/7+…=π/4
という式(ライプニッツの公式)です。
これを式変形し、
π=4/1ー4/3+4/5ー4/7+…
をひたすら繰り返していくことで、円周率の値がどんどん正確になることを意味します。
同様の無限級数はその後も多数発見され、中でも有名なのは1700年代に発見されたマチンの公式になります。
この式は三角関数を含んでしまうので割愛しますが、これで小数第100位まで計算したと言われています。
πの記号が使われるようになったのも、この頃からです。
そして1910年にラマヌジャンという天才数学者が発見した式がこれです。
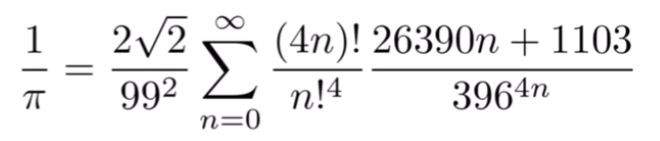
一見すると複雑ですが、シグマ(Σ)の記号はn=0から始めて、1ずつ増やしながら∞(無限)回足し算する、という意味なので、計算自体は大したことありません。
また!(階乗)は、元の数から1ずつ引きながらかけていって、1になるまでかける、という計算式です。
例えば、
5!=5×4×3×2×1
0!=1
となります。
この話をすると

「なんで円周率を求める式がいくつもあるの?違う式だと違う答えになっちゃうんじゃないの?」
と、例外なく言われます。
答えが一つになる計算ばかりやらされている子どもからしたら当然の疑問です。
もちろん答えは一つになります。
当然どの式でも、ひたすら繰り返していけば、同じ計算結果に近づいていきます。
問題は、一般的な式とは異なり、無限級数の場合は答えが出るわけではなく、答えに近づいているだけ、ということです。
つまり、結果的に計算結果は同じ数値に収束していくのですが、その答えに近づく速さが式によって異なるのです。
これを収束速度と言っています。
そしてこのラマヌジャンの発見した円周率の公式は、それまで発見されていたどの無限級数よりも収束が速かったのです。
試しにこの式をn=0で解いてみる、つまり最初の1つだけ解いてみると、いきなり3.141592まで求められてしまうのです。
そしてこの式の面白いところは、ラマヌジャン自身、「夢の中で女神が言っていた式だから証明できない」と言っているのです。
そのため、正しいのかどうかはっきりしない式でしたが、約80年後の1987年にこの式は正しいことが証明されました。
さらにその後、コンピューターが登場により新たな級数が発見されはじめ、1994年にはチュドノフスキー級数が発見されました。
岩尾さんが用いたのはこの式です。
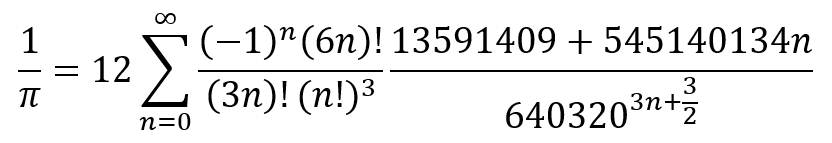
球をぶつけて円周率を求める
2つの重さの球と壁を用意し、1つの球(軽い方)と壁を静止した状態でおいておきます。
その球と壁に対して、もう一つの球(重い方)を転がしてぶつけます。
するとぶつけられた軽い球は転がっていき、壁で跳ね返されて戻ってきます。
そしてまた重たい球に当たり跳ね返されます。
これを繰り返し、何回衝突するかを求めると、円周率の値が求められます。
これは重さの差が大きければ大きいほど衝突回数が多くなるので、円周率の桁もそれだけ多く求められることになります。
この原理については、運動方程式とエネルギー保存の法則が関係しており、その式を知らないと原理の説明もできないため、ここでは割愛しますが、
ボールの質量比が100のN乗:1のとき、円周率の小数点以下N桁目までと衝突回数は一致する
という法則に基づいて計算できるため、決して適当ではありません。
例えば、N=3で計算すると、質量比は1000000:1で、この衝突回数は3141回。
つまり、小数点第3位までの値は3.141となる、ということです。
なぜこんなやり方で円周率が出せるのでしょうか。
端的にイメージだけで話すと、運動方程式は2つの速度を変数とした関数にすると一次関数の式になります。
そしてエネルギー保存の法則の方程式は、2つの速度を変数とした円のグラフになります。
実際には衝突の度に方向が変わり、方程式ではプラスマイナスが逆転することでそれが表され、グラフでは上下反転することでそれが表されることになります。
つまり、直線と円が2点で交わり、ぶつかった点から垂直方向へ移動し、また円とぶつかったところで直線を引き…と繰り返した交点の数が衝突回数ということになります。
とても分かりやすい説明はこちら。(1:32あたりからがこの説明)
さて、なぜここから円周率が出せるのかは、端的に言えば、エネルギー保存の法則の方程式に、円の要素があるからなんですね。
シミュレーションはこちら。
振り子の周期から円周率を求める
振り子も円運動であることから、円周率を求めることができます。
ただし、振り子は大きく揺らしてしまうと他の要因による誤差が出てしまうことから、とても小さな振動(微小振動)でのみなりたつという条件がつきます。
このときの関係は、以下の式で表すことができます。
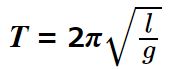
T:周期
g:重力加速度(約9.8)
ℓ:振り子の長さ
この方程式をπ=の形にすることで、円周率を求める式をつくることができます。
実験では振り子の長さを決め、少しだけ揺らし、その周期を測定して円周率を求める式に代入することで求めることができます。
ちなみになぜ微小振動でなければならないのかというと、sinΘ≒Θと近似できるためです。
と小学生に言ってもわからないので、角度を小さくすればするほど、その角度の大きさの数値と、隙間の大きさの数値が大体同じになるから、と説明し、定規で試してもらえばわかってくれるはずです。
45°にすると45cmあくのかというと、そうとも限りませんからね。
このように、円周率を用いて求められる数値を使えば、逆算で実験的に近似値を求めることは可能です。
なので、ばねを用いた単振動でも求めることが可能です。
円周率を求める方法は沢山あるんですね。
でも実験を用いて求めると、どうしても誤差がでてしまうため、正確な値を求めるには精度の問題がつきまとい、詳しい値までは得にくいのです。
番外編
算数の歴史と文化の違い
日本の小学校では3.14と習い、中学校ではπ(パイ)と習いますが、欧米では22/7(7分の22)と習います。
なぜ日本と欧米では異なる扱いとなっているのでしょうか。
その原因は、分数と円周率が伝わった背景にあります。
まず記録に残る形で分数が最も早く用いられているものは、紀元前1世紀頃の漢の時代に書かれた『九章算術』と呼ばれるものです。
つまり、約2千年前にはその原型となるものが登場していたことになります。
そして元々「算」の字は「竹冠に弄(もてあそ)ぶ」という漢字が使われており、竹を用いて計算していたことが伺えます。
日本でも『九章算術』の影響を受けて算術が進化し、平安時代の児童向け教科書『口遊(くちずさみ)』には「曲」、つまり歌として九九を覚えるものが登場しています。
九九を覚える文化はこの時からあったんですね。
そして江戸時代には『塵劫記(じんこうき)』という算術書が登場し、これが全国に広まって算術ブームを巻き起こします。
和算を神社に奉納するようになったのもこの頃からですね。
そしてその本の影響を受けた関孝和(せきたかかず)が点竄術(てんざんじゅつ)を用いた代数学(方程式)を発明し、それを『発微算法』で発表しました。
これが和算を数学へと発展させるための基礎になっており、現在の西洋数学とは異なる発展を遂げた数学を生み出しています。
また、関孝和は円周率へも非常に執着しており、独自の計算(和算)を用いて小数第11位まで計算することに成功しました。
一方西洋でも、アルキメデスが紀元前200年代に、正九十六角形に内接する円を用いて、円周率が22/7よりも小さい値になることを証明しており、さらにそれ以前から22/7は用いられていたようです。
このように、歴史的な背景から西洋では22/7が一般的に用いられ、日本でも分数自体は入ってきていたとはいえ、「三分之一」のように文字で書くためのものだっため、分数を数式として使う習慣はありませんでした。
一応和算には分数にあたる式のようなものがありましたが、そもそも日本は縦書きの文化でしたから、数式も漢字を用いた縦書きだったのです。
現在のようにアラビア数字で表すようになり、記号としての分数を使うようになったのは、明治時代以降なので、割と最近の話なのです。
この影響からか、日本では小数を重視して習うため、分数を習うのが小4からとなっていますが、欧米では小2で分数を習います。
そして円周率は、日本では小5で習いますが、アメリカでは小6で習います。
つまり日本で円周率を扱うとき、分数は習っていない、もしくは習いたてなんですね。
ちなみに欧州では国により分かれていますが、いきなりπとして扱うこともありますし、日本のように小数で扱うこともあります。
いずれにせよ、実際の数値を求めることをそれほど重要と考えておらず、むしろ計算のしやすさを考慮して22/7が使われていると考えられます。
球の表面積の考え方
よく聞かれるので、球の表面積の求め方についてもお話しておきましょう。
原理だけなら等積変形と同じ考え方(カバリエリの原理)で説明できるのです。
もちろん実際に計算で求めるためには三角比や積分を用いなければならないので、ここでは感覚的な話にとどめておきます。
まず円を書きます。
この円の面積は円の面積はπr2(パイアール2乗)ですね。
そしてこの円を、同心円を描きながら細かくドーナツ状にカットしていきます。
このとき、幅は極限まで小さくし、なるべく幅の小さいドーナツを作っていきます。
そしてこのドーナツを、中心に近いほど高く、円周に近づくほど低くして持ち上げていきます。
提灯のように縦に持ち上げて広げていくイメージですね。
こうすることで、円と全く面積が同じ、半球の形を作ることができ、真上から見れば、表面積は円と同じ半球になっているといえます。
しかし、実際には厚みがないものを持ち上げて半球に見立てているため、このままでは横からみると、何も見えない半球となります。
横から見ても半球に見えるようにするためには、横から見えるように、最初のドーナツに厚みを加えなければなりません。
上から見ると円の面積に見えるため、この円の面積の半分(半円)を横から見えるように厚みをつけていくと、横から見た時に半球が作れます。
しかしこれだけでは一方から見た時に半球に見えるだけなので、90°回転させると見えなくなってしまいます。
そこで、縦と横、両方から半球に見えるように厚みをつけていくと、両方合わせて円1つ分の面積を与えたことになります。
これで円の面積の2倍の半球が完成です。
さらにこの半球を2つ合わせれば球が完成し、その表面積は円の面積の4倍となることがわかります。
とはいえ、この方法では想像力が必要となるため、身近なところでそれをイメージできるものがあるといいでしょう。
オススメなのは野球ボールです。
野球ボールは2枚の布を縫い合わせて作られていますが、その1枚の形は2つの円をくっつけたような形になっています。
正確な円ではないので誤差があるものと考慮して考えれば、球は円4枚分でできている、とイメージしやすいでしょう。
なぜ円周率に終わりがないのか

「円周率には終わりがなくて永遠に続くって聞きましたが、なんで終わりがないって言いきれるんですか?もしかしたら終わるかもしれないじゃないですか。」
この質問も塾生からよく聞きます。
そうなんですよね。
全員習ってきているはずなのに、なぜ永遠に続くのか、について教えてくれる先生はほとんどいないのです。
でもここまで考えればもうお分かりですよね。
円周率の求め方、どの方法を取っても、無限に角度を増やすとか、無限に足していくとか、求め方そのものが無限に計算していく手法なので、答えにも終わりがないのです。
このように、一見高校生以上でなければ難しいと思われる計算も、原理だけなら小学生でも理解できるので、本当に覚えておかなければならないことなど、ほとんどないのです。
受験やテストのために暗記するのがいかにもったいないことか、よくわかりますね。
-1024x576.png)






-3.png)


-21-150x93.png)

-3-485x300.png)




-5-485x300.png)






「円周率って何なのかよくわからない。」