早稲田大学高等学院中の算数
早稲田大学高等学院中の算数の面積を求める問題を扱ったのでちょっと紹介。
これも三角形の面積の求め方さえわかっていれば解けるため,小4でも解けるでしょう。

答え:
①12平方cm
②10平方cm
解説ではこれと同じ図形を4つ組み合わせて,正方形の中に内接する正方形にして解くやり方が紹介されていましたが,その解き方ではこの問題しか通用しません。
同じ図形を組み合わせるやり方自体は他の問題でも通用することはありますが,使える時と使えない時が出てきてしまうのです。
そこでどこに注目させるかというと,
・同じもの(相似,合同)
・同じ辺(二等辺三角形)
・同じ角
です。
実は中学受験の図形の問題で,解けない原因の9割はこれに気付けないせいだと言われているのです。
この問題もこれに着目できれば解けてしまいます。
実際に子どもが解いたノートをお見せしましょう。
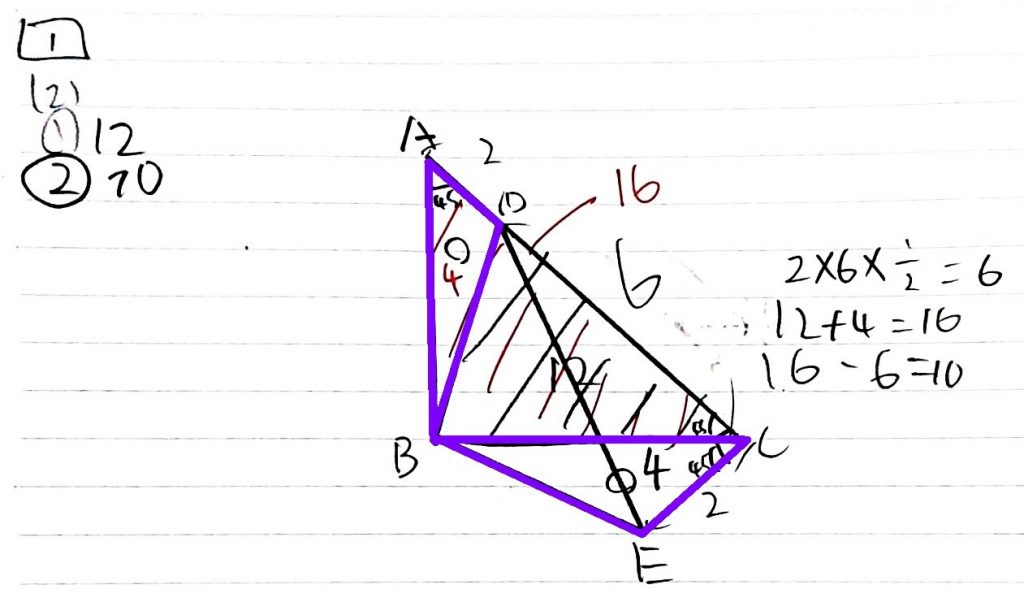
この紫の部分が合同(大きさも形も同じ)になります。
この子も「同じところを探せ」としか指示していませんが,ここまでたどり着き,解いてしまいました。
ただ,正直勘で解いた感じがあったので,どうして同じ図形と言えるのか,まで突っ込みました。
この紫の三角形の内,2つの辺は直角二等辺三角形の辺の一部なので同じ長さになります。
そして両方とも直角三角形ということは,∠ABDと∠CBEは同じ角度という事になります。
中学生では合同条件として習いますが,中学受験では名前が出てきません。
しかし,何となくで解かせないようにするには,合同条件まで教えてしまう方がいいでしょう。
そこまで堅苦しく考えなくても,実際に条件を与えて作らせてみれば,どういう時に同じ三角形になるのかすぐにわかってくれます。

実はこの子の場合はここまではサッと説明してくれました。
ところが,∠ECD=90度という所の方で説明が詰まってしまったのです。
すごく簡単なのに(^^;
しばらく考えましたが出てこない…
こういう時はわかる角度を書き込むことで再認識できます。
そこで「わかる角度を全部書き込んでみて」と言ったら,数秒ですぐに解決しました。
解けるか解けないかの差なんてそんなものです。
沢山数をこなしているのに一向に解けるようにならない子と,全然数をこなさなくても気付けるようになる子の差は,その問題の解法を覚えることに終始しているか,どういう問題でも解けるやり方を学んでいるかの差から生まれるのです。
解説の解き方が必ずしもお子様に合っているとは限りませんので,解説の解き方を押し付けないように注意して下さいね。
理想は,その子の思考回路に無理のない解き方を修得することです(^^)/









-24-485x300.png)
-4-485x300.png)










コメントを残す