昭和秀英中　算数：分数の計算・規則性

昭和秀英中　算数　入試問題

対象学年：小４～中３

昭和秀英中というが学校の中学入試の問題を塾生が受けて来て、みんなで解いてみたのでちょっと紹介しましょう。

千葉県の蘇我教室、西船橋教室からは毎年受験者がいる、千葉四天王と呼ばれる、市川、東邦、秀英、渋谷幕張の内の１つです。

都内難関を受ける子も受ける学校です。

今回は算数の問題の中でも、分数の問題を紹介しましょう。

分数の計算ではありますが、

• 等差数列の和
• 分数の整数部分と小数部分の関係
• 規則性

といったことを学べます。

小４でも分数の足し算をやっていれば解けるので、やってみる価値はあるでしょう。

中学生でも、等差数列の和や規則性を知っていると、数学でも役に立ちます。

問題　算数：分数の計算・規則性

ポイント

オ：等差数列の和

分母は全て４でそろっているので、通分の必要はありません。

そのため、小４でも分数の和を知っていれば、

5+10+15+…+200

を計算して、それを4で割るだけで答えを出せます。

この時、この等差数列の和を小４ならば地道に計算させて構いません。

全部で40個しかありませんから、大して難しくないでしょう。

解いた後に、簡単に解ける方法があるといって、考えさせると、結構思いつくものです。

これが等差数列の和を解く受験テクニックの修得につながってきます。

カ：分数の整数部分、小数部分、規則性

この問題、子どもは整数部分はすぐに出せることに気が付いて、答えの1025から整数部分を引いて出そうとします。

もちろんそれでも構いません。

大切なのは実際にやってみること。

それでやってみると、このようになります。

これは実際に塾生に考えさせたやり方。

このように小４でも十分できます。

でも実際にやってみると、４つおきに間が抜けているちょっとめんどくさい。

そこで他のやり方はないか考えさせてみます。

すると、小数部分をそのまま足すという方法でやってみると言い出しますので、小数部分を分数のまま書き出させてみます。

それがこれ。

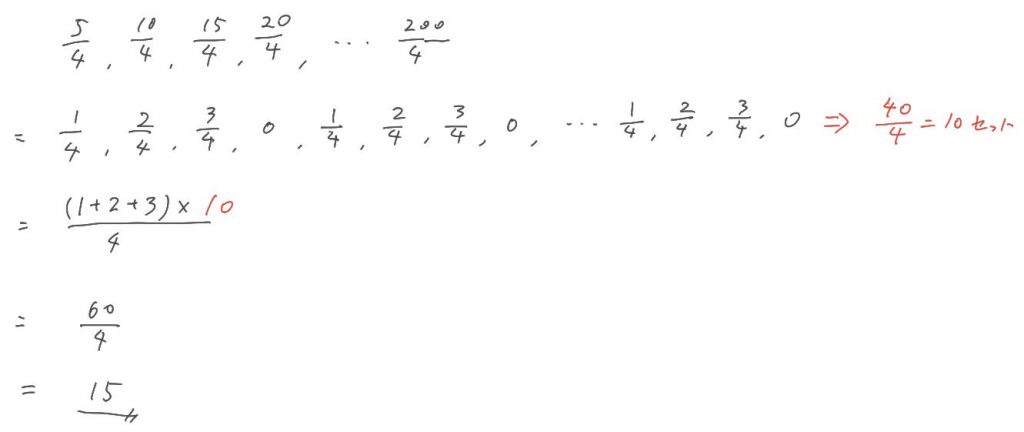
小数部分だけにして分数を並べてみると、４個１セットの同じ規則で並んでいるだけなんですね。

あとはこれを合計するだけ。

このやり方もやはり小４でもできます。

昭和秀英中に合格したいなら

この問題を学ぶときのポイントは、とにかく書き出して規則性に気付かせること。

そして規則性から簡単に計算する方法を考え出させること。

中学受験ではとにかく公式に走りがちですが、公式何て使わなくても出ますし、公式を使わずに解ける子の方が伸びしろが大きくなるのです。

分数の計算さえできれば解けますので、この１問を通して、じっくりと学んでみて下さい。

何度解いても解けるようにならないなら、それは勉強法が間違っている証拠。

その時はファイへご連絡下さい。

現在はオンラインで全国の生徒を指導しているファイですが、創業は千葉県の蘇我。

昭和秀英中は蘇我からも沢山受験しており、経験も豊富なので、秀英への近道をアドバイスできますよ(^^)/