渋谷幕張中の算数の過去問「整数問題」を解いてみよう

渋谷幕張中　算数　入試問題

対象学年：小４～中３

千葉県の最難関中学校、渋谷幕張中で出題された問題をちょっと紹介しましょう。

最難関の問題ならすごく難しいんじゃないかと思いきや、実はレベル的には割り算の計算さえできれば解けてしまうため、小４でも解けてしまいます。

難しい理由は、いわゆる中学受験用の特殊算を用いるタイプではなく、整数の性質に着目して推理していく必要があるため。

公式の丸暗記では解けないため難しく感じるのです。

実際ファイの小４にも解かせてみましたが、ファイでは公式を暗記させていないため、解けてしまっています。

なお、最初にネタバレしておくと、この問題は高校数学の「極限」にあたる問題です。

よって中学生でもこの考え方を身に着けておくことに十分意義がありますので、ぜひ解いてみて下さい。

問題　算数：整数問題

ポイント

(1)　規則算

この問題は、問題の意味をちゃんと理解しているかの指標になります。

一見複雑そうな問題ですが、実はたいした規則ではありません。

与えられたルール通りに式を立てて計算できるかどうかがカギとなります。

式が立てられていない場合には、問題文を１つずつ読み解く練習が必要でしょう。

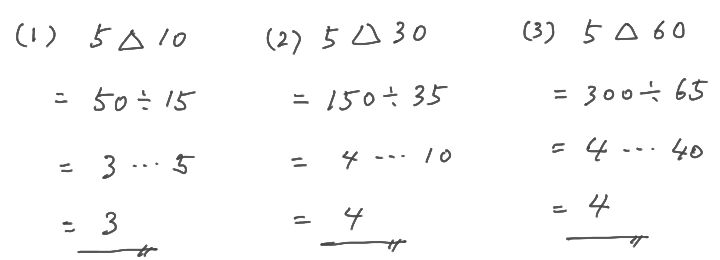
(2)　極限

この問題は、Cにはどんな数が入ってもいいということなので、適当な数を入れて試すことができるかがカギとなります。

一応（１）もヒントになっていますね。

例えば、cに10000を入れて計算したらどうなるでしょうか。

割られる数は8×cなので、80000になります。

そして割る数は8+cなので10008になります。

これを割ると、約８倍ですが、微妙に８倍よりも足りていないため、7.…という数になります。

そしてcの値をさらに大きくして言っても、限りなく8に近づいてはいくものの、8には絶対に到達しません。

この絶対８には到達しないという部分に気付けるかがポイント。

この実際に数字を入れて試して見ることをサンプリングといい、中学受験だけではなく、数学でも大いに役立つテクニックになります。

(3)　推理

余りが３になると言っているので、実際に式を書いて、当てはまる数を探していけば答えが導けます。

これもとやかく考えるよりも、まずは手を動かせる子なら解けてしまいます。

もう一つのポイントとなるのは、３△ｄの値がどうなるか。

これは（２）と同様に考えれば、最大２にしかならないということになります。

つまり、３△ｄの答えば、０か１か２しかありえない。

ここまでたどり着けば、あとは大したことないでしょう。

答えとなるｄも３つ。

あとはこの３つをそれぞれ使って、逆算してあげれば答えが３つ出てきます。

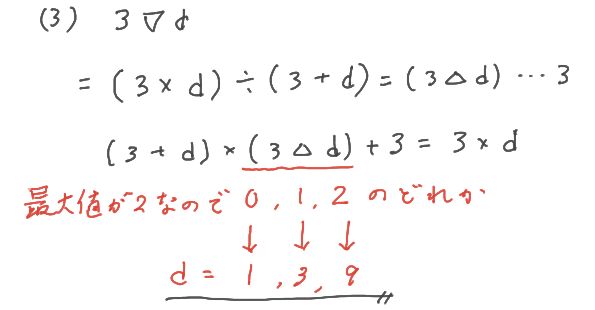
渋谷幕張中に合格したいなら

渋谷幕張中は千葉県で最難関の学校とはいえ、実は問題自体は大して難しくありません。

この問題もそうですが、一見複雑そうに見えても、実はたいしたことない問題が多いのです。

渋谷幕張の問題が難しいと感じてしまうのは、公式に頼った問題演習ばかりしているからなんですね。

ファイでは過去に何人も合格を出してきていますが、その内３人ほど特待で合格しています。

そして面白いことに、特待を取ったにも関わらず、模試で一度も合格判定を取ったことがない(笑)

ファイではこのように一つの問題にじっくり向き合って、本質を学ぶ勉強をしているため、渋谷幕張の問題は大して難しく感じないのです。

そしてもう一つ。

ファイでは学年の枠を超えた勉強をしてしまいます。

渋谷幕張の出題も、学年の枠を超えた内容がポイントとなっていることが多いので、ファイト問題との愛称がいいんですね。

もし渋谷幕張を狙うなら、公式の丸暗記ではまず通用しません。

暗記ではなく、数や式の本質を見抜ける勉強の仕方をしていって下さい。

どうもうまくいかずに公式の丸暗記に走ってしまっている方は、ファイへご連絡下さい。

公式や暗記に頼らない勉強法を身に着けていきましょう(^^)/