市川中の算数：単位分数の和

市川中の単位分数の和

「２１分の１３」という分数を単位分数の和で表せという市川中の入試問題。

問題文中には例として「７分の５」を単位分数の和にする方法が書いてあるので，その通り操作をしていけば簡単に解けます。

ただし，操作の意味がわからないと解けません。

まず引っ掛かる部分はここです。

この「２分の１」がどこから出てくるかわからない。

これは「７分の５」の分母と分子，両方を５で割ると，「１．４分の１」となります。

要するに通分と同じ操作で分子を１にしたということです。

そして単位分数の和にするということは，最初の７分の５よりも小さな数の和にするということです。

つまり，「１．４分の１」より小さい数を，分母分子両方とも整数にして作ると「２分の１」という数になります。

イメージが湧きにくいと思うので，ちょっと例を。

ホールケーキをカットケーキの組み合わせで作るとき，カットケーキの大きさは確実に作るホールケーキよりも小さなものの組み合わせで作ります。

このカットケーキの大きさは何でもいいわけではなく，５等分とか７等分とか，整数個に分けたものを使わなければなりません。

先程の例ですと，１．４分の１というケーキのカットはできないため，切りたいサイズに近い，２等分した「２分の１」というサイズにして切ることになります。

もし「３．２分の１」なら「４分の１」ですね。

そして「２分の１」が出たら，残りは「１４分の３」。

これはまだ単位分数になっていないので，また１４分の３に近い単位分数を探し，あとはこれの繰り返しで単位分数の和を探していきます。

すると最終的には以下の様になります。

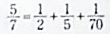
これがわかれば最初の問題が解けます。

これは分数の性質が分かっているかが問われる問題なので，分数の基本さえやっていれば小５くらいでも解けてしまいます。

単位分数の出し方を身に着けるのが目的ではなく，与えられた操作の例から解き方を理解できるか，分数の性質を理解しているかが問われているので，覚えさせないようにして下さい。

ＰＨＩで生徒が解いたのは以下のノートです。