算数・数学の応用問題が解けない場合

基本はできるのに応用ができない

算数や数学で、基本は解けるのに応用になると全く解けないという子。

単純に応用問題を練習していないという可能性もありますが、応用問題をいくら練習しても解けないケースがあります。

ファイのオンライン教室でその実例がありましたので、ちょっと紹介しましょう。

式まで合っているのに答えまで出せない

ちょっと市川の入試問題を解いたノートを見てみましょう。

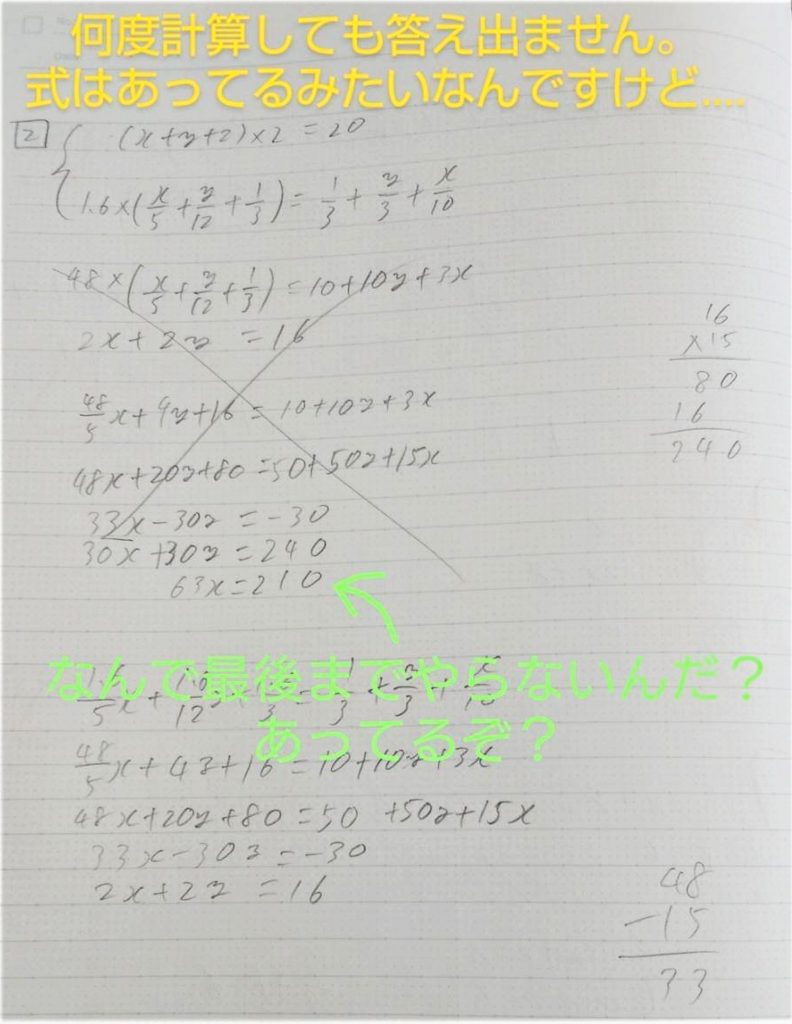
これが数学の連立方程式の問題を解いたノートです。

何度やっても答えが出ないと言って送ってきたのですが、毎回同じところで止まっているのです。

しかしこれ、ここまであっているのです。

式まで立てられて、解くだけになっているのに、解の目前で立ち止まってしまっているのです。

行って見たいお店があって、目の前まで行ったのに入らずにうろうろしている感じですね。

このまま解けばいいのに。

でもそれが出来ない子が結構いるのです。

基本に慣れすぎている

基本問題に慣れすぎていると、答えが整数になる問題ばかりなため、分数や小数の答えになると突然不安に駆られてしまうことがあるのです。

「基本ができれば応用ができる」とは限らないのです。
かえって基本ばかりやっていることで、応用問題が解けなくなる壁を作ってしまうこともあるんですね。

過去問をやればわかりますが、学校によっては答えが切りのいい数にならない問題を多く出す学校、理科の実験の問題では誤差を含んだ問題を出す学校。
難しい学校になればなるほど、綺麗な数にはならない事が多くなってきます。

そのため、小数や分数の答えになることもあるという経験をさせておかないと、不安に駆られて答えまでたどりつけないのです。

しかしこれをテストで解くと、点数は０ですから、一見すると解けていないように見えてしまいます。

今回は応用が解けてない一例を紹介しましたが、応用が解けない理由は様々。

なぜ解けていないのか、しっかり分析した上で攻めていかないと、やってもやっても難しい問題で点が取れるようにはなりません。

学習法診断にて分析できますので、うまくいってないようならご相談下さい(^^)/