開智日本橋中の算数：図形

開智日本橋中の図形問題

パズルみたいな問題を扱ったので，その問題を紹介。

わかってしまえば大したことないので，三角形と角度さえ知っていれば小４でも解けます。

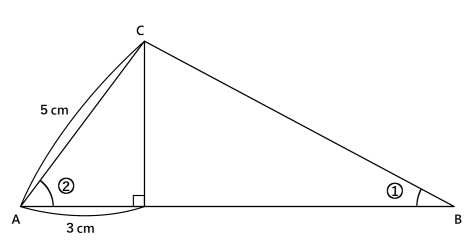
図のような角度の比が１：２となっている三角形ＡＢＣの底辺ＡＢの長さを求めなさい。

答え：１１ｃｍ

この問題は解答ではこのように解く解き方が紹介してあります。

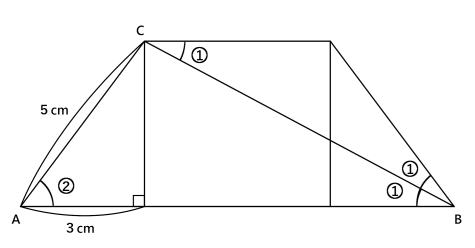
このように，右側に左側と同じ三角形をつけて，つないでみると，二等辺三角形ができます。

そのため，３＋５＋３＝１１ｃｍとなるのです。

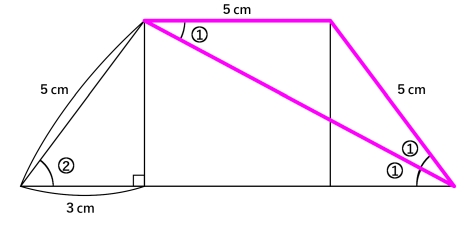
確かにこの解き方は美しいのですが，この解き方ではパズルのように，何もない所に自分で図形を作り上げていかねばならず，考えても知っていなければ解けない問題なのです。

もっともパズルのように図形に接してきた子なら，あれこれ試しているうちに見つけられるかもしれません。

しかし入試として解くなら，現実的にはパターンの一つとして覚えるということになってしまいます。

そこで，パズルが思いつかなくても，今までの考え方で解ける方法をご紹介します。

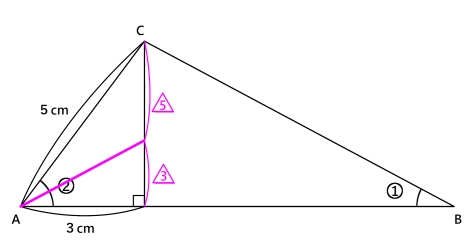
２倍だった角の二等分線を引き，垂線を３：５に分けます。

この方法も角の二等分線が底辺を，他の二辺の比でわけることを知っていなければなりません。

しかしこの方法なら他の問題にも使えるので，汎用性があり，考えて解けるようになります。

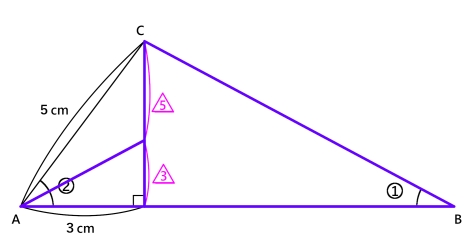
角の二等分線を引くと，この青い三角形が相似になります。

ということは，

高さが△３の三角形の底辺　⇒　３ｃｍ
鷹さが△８の三角形の底辺　⇒　？ｃｍ

となるので，？の部分は８ｃｍとわかります。

よってＡＢ＝３＋８＝１１ｃｍとなります。

この問題も，この１問をしっかりと突き詰めれば，様々な問題を解けるようになります。

予備知識が必要という意味では入試問題としてふさわしいとはちょっと思いませんが(^^;

練習としては思考力を鍛えることができる良い問題なので，ブレイクタイムにでも子どもと一緒に考えてみて下さい(^^)/