東邦中の算数:速さ
オンライン授業で、東邦中の過去問を扱ったので紹介しましょう。
東邦中は千葉県にある私立中学で、理系が難しいことで有名な難関中の一つです。
指導したのは小5で、単元は速さです。
300m
鉄橋を渡る問題もトンネルを通過する問題も、列車の長さを加味しなければならないため、長さと速さの関係を押さえるのに適しています。
また、基本的な問題では速さ、もしくは鉄橋かトンネルの長さがが決められてしまっていますが、この問題は速さも長さも出ていないので、比を使わなければなりません。
つまり、消去算なり倍数変化算なりを使わなければならないということ。
それらが融合しているので、この1問をじっくり解くだけでも、50問分解くぐらいの多くのことが学べます。
実際に指導した時のノートがこちら。
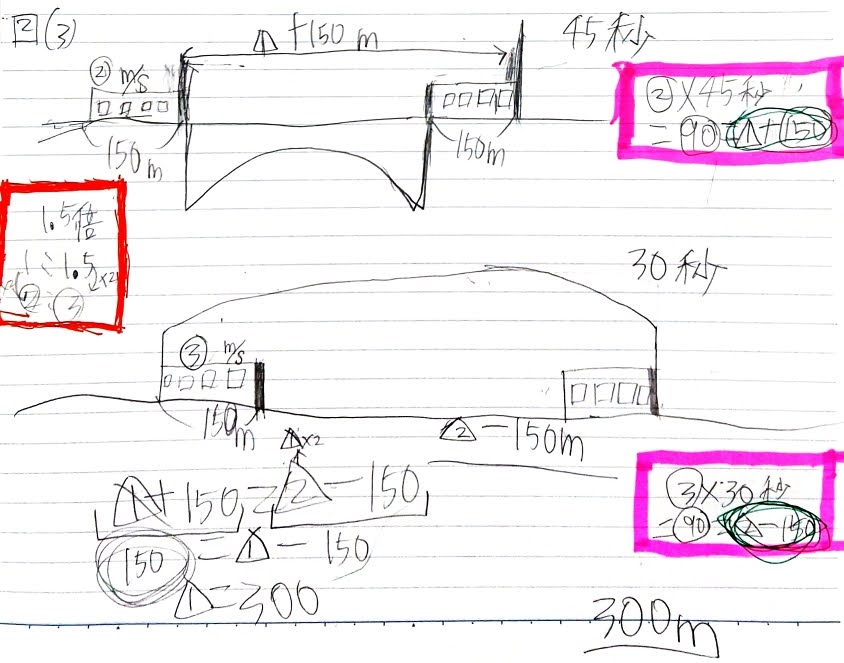
この子には、速さ、比の基本的な単元は教えてあったので、鉄橋を渡る、トンネルを通過すると言う部分と移動距離との関係について理解できるかがカギでした。
そのため、図を書かせ、どこからどこまでが移動した距離かを書いてもらいました。
ここで、電車の先頭から先頭ということがわかれば、この問題は解けたも同然。
この子は太く書いてわかりやすくしています。
ここまでわかればあとは長さの関係を式にするだけ。
この子は式の理解が強いタイプなので、この問題に限らず、通常は立式を軸に解く解き方を指導しています。
立式が苦手な場合は、書き出しや線分図にして解く方法もあります。
正直立式が早いのですが、得意な方法で解けるようにしておく方がいいでしょう。
結局、どう解くかで大切なのは、その子の思考回路に無理のない考え方で溶けるやり方を身に着けておくことなんですね。
この子も移動距離がわかってしまえば、立式がすぐにでき、この子は消去算で導いてしまいました。
東邦中は難しいと思い込まずに、難しい問題を1問しっかり理解した方が、数をこなすよりも理論に強くなります。
そして理論に強い子は、中学、高校と進学するにつれてスピードのみの子に勝っていきます。
速さは顕著にそれが表れる単元ですから、ブレイクタイムにでも1問解いてみるといいでしょう。
東邦の化学
次にオンライン授業で東邦高校の化学の過去問を扱った時の話をしましょう。
元々わからないと言っていたのは中学生なのですが、ファイのオンライン授業では、学年を問わず受講できるので、中学受験の小学生も一緒に受けています。

「化学反応式がわからないのではないでしょうか…?」
確かに小学校では化学反応式は習いません。
しかし、中学受験の塾では教えてしまっている所も多いんですね。
なのでそこそこ知っていることが多いのです。
ファイでは、知っていれば使ってしまいますし、知らなければ使わずに説明してしまいます。
いずれにしても、化学式を使うかどうかだけで、中学受験も高校受験も問題は同じなのです。
特に計算問題の根本原理に関わる部分に関して言えば、全く同じです。
だから、小中学生が一緒に勉強しても、全然問題ないんですね。
さて、化学と言えば、化学式に化学反応式,、酸化還元反応、中和滴定など、計算問題がつきものです。
化学の問題は中学受験でも高校受験でも、どの学校でも基本的に毎年必ず出題されるものの、問題の出題パターンが多く、暗記では対応しきれない問題が多いのです。
だから難関を目指す子にとっては、とにかく苦労する分野の一つなんですね。
この子の指導前の初期レベルは簡単な問題にもかかわらず、(1)から間違えるこのありさまです。
当然計算問題なんてできるわけがありません。
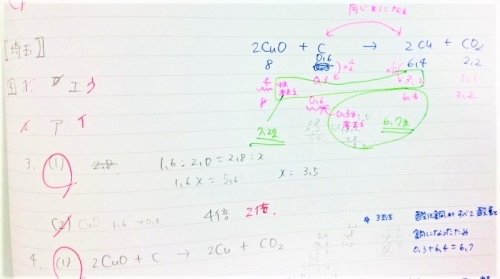
他の基本的な化学もやっていますが、軒並みダメ。
全問解けた過去問はほぼ皆無。

「もー意味がわからない。アルミって塩酸以外で溶けるんですか?」

「そこ!?それ小学生でも知ってるでしょ。」

「この解答見ると、水酸化ナトリウムでも溶けてるんですよ。」

「そりゃそうだろうねぇ。」
こんな会話がスタート(笑)
でもですね、そろそろ頃合いだと言ったのはこういうことです。
この子は化学を解くにあたって、ある思考パターンを身に着けてきました。
知識はない。
しかし考える力はついています。
だから知識を入れてあげれば・・・

理科では全国有数の難しさ、東邦の化学が全問正解!\(^o^)/
もちろんほぼ自力です!
一問、一言だけ方針でヒントは出しましたが、まぁわかる人じゃないとわからない程度の些細なヒント。
もちろん誰でも簡単に1日でこのような事ができるわけではありません。
ここまで持って来るための思考の下積みに相当な時間と労力を費やしていますからね(^^;)
しかし時間がかかっても「考える力を身に着ける」という事は、こういう可能性が広がるということなのです。
実際この子は化学に限らず、次々と習得分野を広げています。
あとは入試までにどれだけ埋められるか。
この境地まで来ると、もうどんどん伸び続けそうな気がしますが、実はもう一段階あるのです。
それが「突然視界が開ける感覚」です。
根詰めて徹底的に取り組んだ時、なんだかどんな問題でも解決できてしまいそうな感覚に陥ったことありませんか?
あの感覚です。

「なんかね、答えが見えちゃうの!」

「頭で考えているというより、手が答えを書いていってるの。」

「突然試験時間に余裕ができるようになったよ!」

「気付いたら勘で答える事がなくなってました。」

「朝も昼も夜も、歩いてる時も寝てる時も、ずーっと何かの問題を解いているような感覚です。でも全然疲れないし、それが普通だし、むしろ楽しい気がします。」
表現の仕方はさまざまですが、ファイのオンライン授業では毎年何人もこのような発言をしています。
この急に視界が開ける感覚を経験してからが本当の爆発的な伸びにつながります。

「もう限界、もう限界、と思ったその先に答えがある。
『もう限界』が『まだ行ける』に変わった時に、彼女にも見えそうですね、その世界。」
と、この子の先輩が言っていました。
考える勉強って、こういう瞬間があるから面白いんですよね。
東邦中の算数:相似問題
次に、オンライン授業で東邦中の相似の問題を扱った授業を紹介しましょう。
解いたのは5年生です。
東邦中というとガッツリ理系の学校ですが、最近はだいぶ丸くなってきており、複雑な計算を必要としなくなってきました。
この問題もそんな問題の一問で、根本原理が分かっていれば解ける問題です。
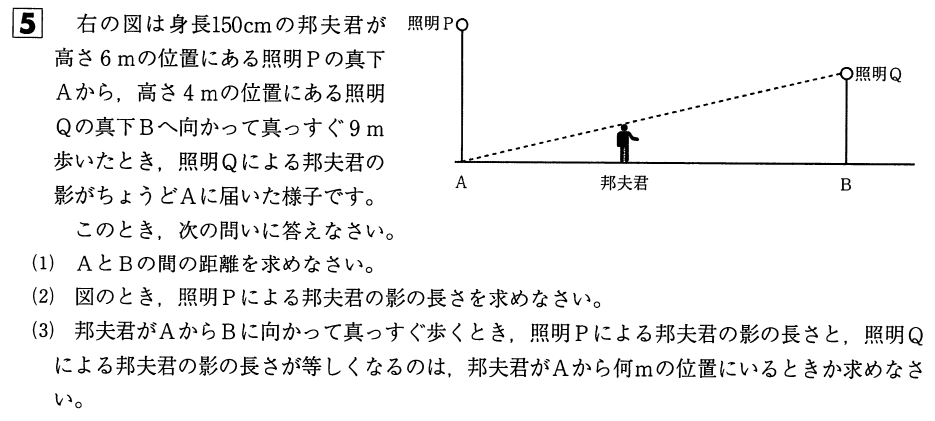
(1)24m
(2)3m
(3)108/7 m
この問題はまず問題文で言われていることを書き込む力が試されます。
この時点で書き込めない子が結構いるので、もし書き込めていなければ、まずはわかることを書き込ませて、相似をみつけさせます。
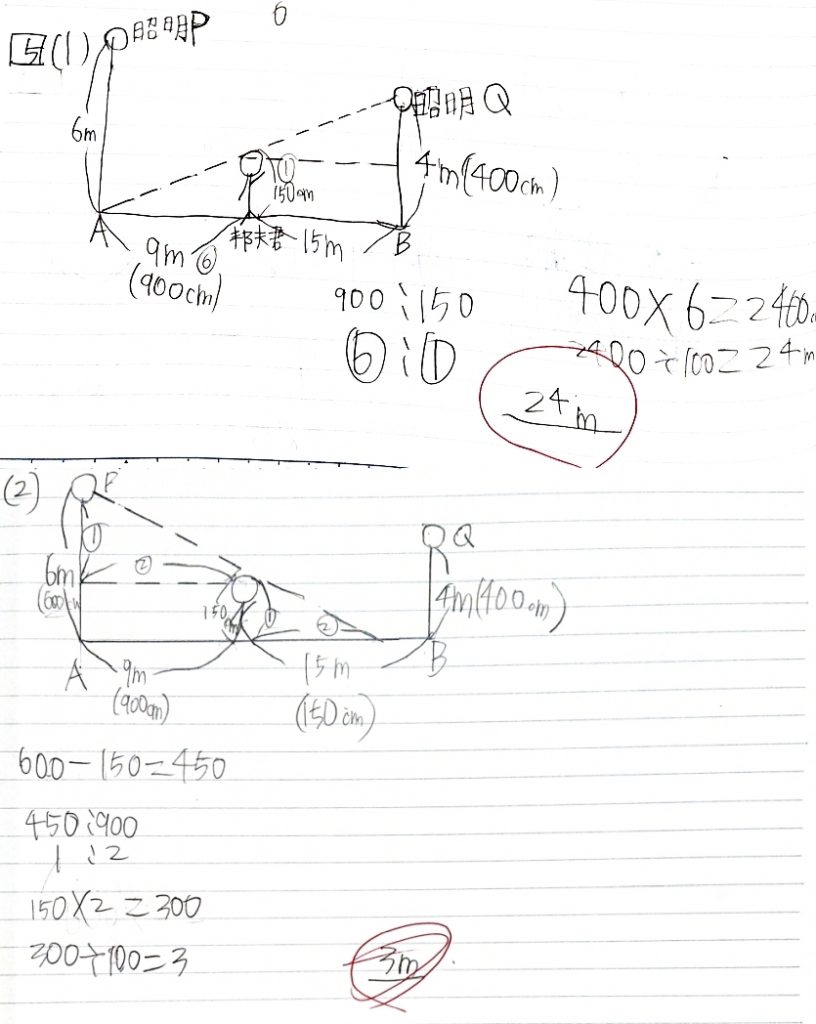
このように書き込んでしまえば相似に気付きやすくなります。
もし相似をやっていなければ、書き込んでも解けないため、ここで一度相似の性質について簡単に触れます。
1からガッツリやる必要はありません。
この問題を解くにあたって必要な知識だけを補足してあげれば十分なのです。
この子の場合は既に相似を教えてしまっていたので、特に改めて教えていません。
相似が理解できていれば、後は計算するだけなのですが、どこの相似を利用するかによって、簡単に求められるか、面倒になるかが決まります。
この子の場合もどこの相似を使えばいいかわからなくなってしまっていたので、人の頭の部分から街灯に向かって地面と平行に線を引くようにヒントを出しました。
こうすると相似な三角形がもう一つ増え、この三角形の辺の比を用いれば、2辺とも長さがわかるため、簡単に導くことができます。
この子もこの線を引かせただけで、相似な図形を見出し、自分で解くことができました。

この1問さえしっかり理解できれば、ほとんどノーヒントで(2)も(3)も解けてしまいます。
もし芋づる式に解けない場合は、相似の理解が甘い可能性があります。
サンプルとして載せたこのノートには(3)がありませんが、(3)は「最初と後の状態をそれぞれ図にする」というヒントを与えただけで解けていました。
相似は何度も練習しないと解けるようにならないとよく言われますが、それは相似を見つけて計算するまでの話です。
どこの相似を使って、どう解くか、については別のテクニックが関係してくるのです。
これに関しては、数をこなすよりも、自分で見つけ出した経験の方が身に付きやすいので、教え込まずに自分で気付けるようにサポートしてあげるのがいいでしょう。
この子のように、ガツガツやらなくても解けるようになります。






-1-1024x576.png)
-3-1024x768.png)















長さ150mの列車が鉄橋を渡り始めてから渡り終わるまでに45秒。
同じ列車が1.5倍の速さで鉄橋の2倍の長さのトンネルに完全に入ってから出るまでにかかった時間は30秒。
この鉄橋の長さを求めなさい。