渋谷幕張中の算数の過去問「場合の数」を解いてみよう

渋谷幕張中　算数　入試問題

対象学年：小４～中３

千葉県の最難関中学校、渋谷幕張中で出題された問題をちょっと紹介しましょう。

最難関の問題ならすごく難しいんじゃないかと思いきや、実はレベル的にはデジタル時計の表記さえ知っていれば解けてしまうため、小４でも解けてしまいます。

難しい理由は、そつなく書き出せる力が必要なため。

思いつくままに適当に書き出しても解けないのです。

実際ファイの小４にも解かせてみましたが、やはり書き出しに苦労していました。

小５は慣れているので、ほとんどヒントなしで答えにたどり着いています。

中学生でいうところの「場合の数」に当たるのですが、公立ではここまで複雑な整理は必要とされません。

しかし難関私立ではやはり整理して書き出していく技術が問われる学校もあるため、中学生でも解いておく意味は十分あるでしょう。

問題　算数：整数問題

ポイント

(1)　場合の数

まずそれぞれの数字のライトがいくつ点灯しているかを書き出します。

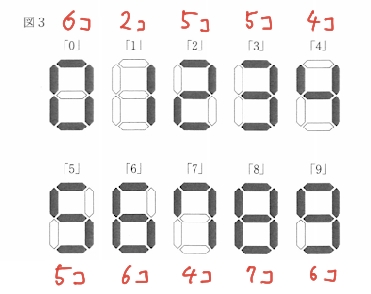
この中で一番多くライトを使っているのは８ですが、４か所全てに８を使う訳にはいきません。

そこで８の次に多いものを探すと、０・６・９。

６と９は８と同様に十の位には入れられないため、０を入れる。

ここでのポイントは、ライトが多い数字を使って実際に書き出させてみることです。

ヒントもへったくれもありません。

まず時間をかけてでも自分で書き出せなければ、このタイプの問題は解けるようになりません。

(2)　場合の数

これはライトが全部で１２本になる組み合わせを考える所から始めます。

ちょっと試してみればわかるのですが、１つの数字でライトが５個も６個もついてしまうものは使えないんですね。

４つ数字を並べる前に１２個を超えてしまいますので。

それに気付けたら、どういう組み合わせなら１２を作れるかがわかるはずです。

渋谷幕張を受験するなら、このぐらいは書き出して解けるガッツは育てておきたいところです。

この程度で気がめいっているようでは太刀打ちできません。

(3)　場合の数

これはファイの小５でも結構引っかかっていましたね。

４～５個までは見つけられるのですが、６個目が出てこない。

まずは数字が１つ増えるとライトがなるべく多く増える数を探します。

すると１⇒２と７⇒８で３個増えるのが一番多いことにすぐ気が付きます。

しかし、これを分の場所に使うと、３個しか増えません。

分の場所は５９⇒００にすることにより、１個稼げます。

後は時間の方に、繰上りで１⇒２と７⇒８になる数を入れる。

これで５個は出ます。

問題はあと１個。

１９⇒２０も実は３個増えるんですね。

これに気付くまで粘りたいところ。

「二けたで考えてみては？」

というヒントを上げると結構気付くものです。

渋谷幕張レベルに対応する力をつけるのであれば、やはり教えるよりも、自分で気が付かせたいものですね。

渋谷幕張中に合格したいなら

渋谷幕張中は千葉県で最難関の学校とはいえ、実は問題自体は大して難しくありません。

この問題も書き出せさえすれば、小４でも解けてしまいますからね。

渋谷幕張の問題が難しいと感じてしまうのは、公式に頼った問題演習ばかりしているからなんですね。

ファイでは過去に何人も合格を出してきていますが、その内３人ほど特待で合格しています。

そして面白いことに、特待を取ったにも関わらず、模試で一度も合格判定を取ったことがない(笑)

ファイではこのように一つの問題にじっくり向き合って、本質を学ぶ勉強をしているため、渋谷幕張の問題は大して難しく感じないのです。

そしてもう一つ。

ファイでは学年の枠を超えた勉強をしてしまいます。

渋谷幕張の出題も、学年の枠を超えた内容がポイントとなっていることが多いので、ファイト問題との愛称がいいんですね。

もし渋谷幕張を狙うなら、公式の丸暗記ではまず通用しません。

暗記ではなく、数や式の本質を見抜ける勉強の仕方をしていって下さい。

どうもうまくいかずに公式の丸暗記に走ってしまっている方は、ファイへご連絡下さい。

公式や暗記に頼らない勉強法を身に着けていきましょう(^^)/