規則性の入試問題を解いてみよう。小学生でも解ける高校入試数学

千葉県公立高校　2021年　数学

対象学年と目的

小５～中３

高校入試の問題ですが、規則性なので小学生でも解くことができます。

ただし、問題文中のアルファベットが読め、代数を表していることがわかる必要があります。

中学受験では〇とか△でおく記号の代わりですね。

小学生にチャレンジしてもらいたい問題は（３）なので、（１）（２）は飛ばしてしまっても問題ありません。

飛ばしても解くことができます。

高校入試の問題にあえてチャレンジする理由は、よくわからない言葉が並んでいても、問題自体は大したことがない典型例だからです。

そのため、問題文は保護者が補足説明を加えてあげれば十分解くことができます。

これが実感できると、問題文を整理して読んでいくことの大切さが理解できるでしょう。

なお、文字を使って解くなら、中１夏ぐらいに文字式を習ってからなら解けるでしょう。

あまり文字式の使い方に慣れていないと、小学生の解き方の方が早いこともあります。

補足説明

この問題を扱うポイントは、解くことではなく、問題文を理解させることにあります。

小学生は（３）のみでOK。

問題文中の「A、B、C、D」は「あ、い、う、え」に置き換えて、m、nを〇、△に置き換えれば中学受験でも解ける問題になります。

また、自然数：１，２，３，といった小数でも分数でもない数

20未満：19までの数

と解釈しておけば解くことができます。

このまま渡しても解けないので、補足説明を加えながら理解させてあげて下さい。

問題文さえ理解できれば解くことができますので、問題文の解釈のサポートに徹して気付かせてあげて下さい。

問題

解答

子どもに教えるときのポイント

まずはこの規則通りに表が書けるかどうか試して下さい。

最大19行目までなので大した量ではありません。

表が正しく書けていれば、ルールの読み取りはできていることになります。

次にm段目の最小の数がB列に来ているのは何段目なのかを書き出します。

そしてn段目の2番目に大きな数がB列に来ているのは何段目なのかを書き出します。

ここまでできれば、それぞれの該当する場所の数字を書き出します。

あとはｍ段目とｎ段目の数の組み合わせが１２の倍数になるものを探すだけ。

全部書き出しても『４個×５個＝２０通り』しかありません。

この中で１２の倍数となるのは７個となります。

もっと簡単に解く方法

最初からこの方法に気付くのは難しいので、まずは書き出して解いてから、規則に気付かせていくのがいいでしょう。

書き出して解いた後に、あまりと段数との関連を考えてみます。

ｍ段目の一番小さい数というのは、一つ上の段の数より１大きい数とも考えられます。

式で書くなら、『ｍ－１段目の最大の数（４の倍数）＋１』ですね。

ｎ段目の２番目に大きな数は『４の倍数ー１』です。

ということは、ｍ－１段目の数とｎ段目の数を足すと、＋１とー１で相殺されるので、４の倍数になることがわかります。

よって段数だけの和は３の倍数となります。

言葉で説明するとわけがわかりませんが、図に書き込んでみればすぐわかります。

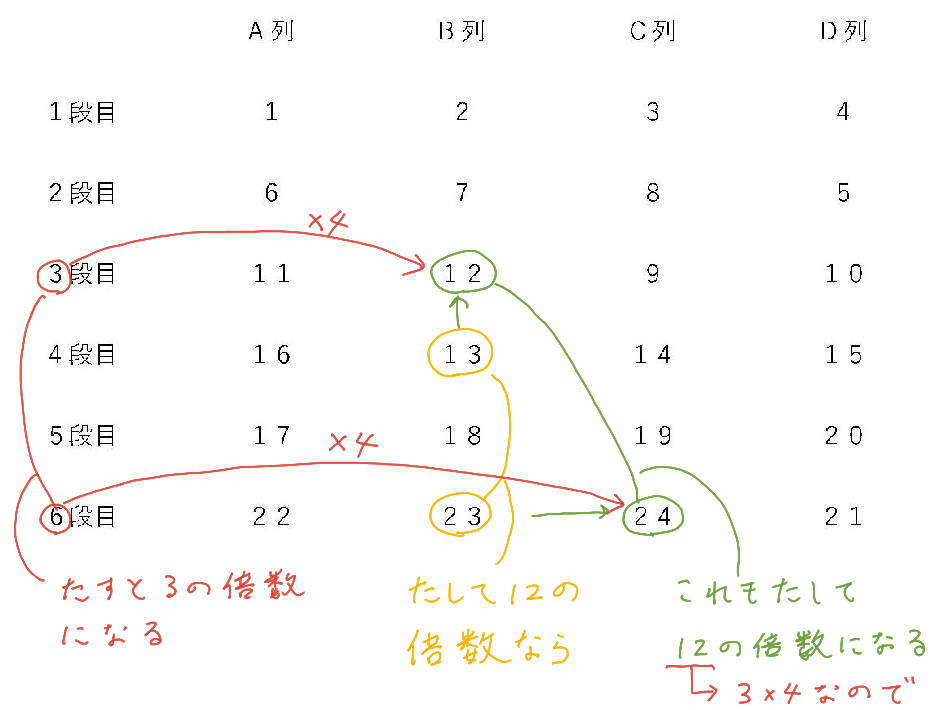
これを整理すると、

この２つの数字の和が３の倍数になるものを探せばいいのです。

すると、

• ３＋６
• ３＋１８
• ７＋２
• ７＋１４
• １１＋１０
• １５＋６
• １５＋１８

となるので７個となります。

高校受験を見据えて今できること

高校受験では方程式を使えるため、小学生とは解き方が異なります。

今回の解き方も小学生向きの解き方をしましたが、中学生なら最初から文字式で押していくことになります。

しかし、数学とはいえ、規則に気付ける力、規則を体系化する力は中学受験で必要とされる力と同じ。

小学生でも解ける問題を、数学として解くことを要求しているだけものが多いのです。

「中学受験はしないから」という理由で受験用の問題を避けている方が多いようですが、中学受験はしなくても、受験の問題に触れておくこと自体には大きな意味があります。

また、中学受験をする子にとって、高校受験の問題をそのまま解くのは確かに難しいのはわかります。

しかし、「問題さえ読み解ければ小学生でも解ける」という実感を持っておくことは、難関校を受験するにあたっては十分意味があります。

難関の問題が難しいのは、問題文を読み解くのが大変で、諦めてしまう子が多いためですからね。

ぜひ学年の思い込みで制限をかけてしまわず、自分が今持っている知識で解き切る経験を積んであげて下さい。

親がついていないと大変な訓練ではありますが、こういう経験を積んでいる子は知らない問題を解くことに抵抗がなくなってきます。

するとこんなこともできるようになるんですね。

塾なしで中学受験勉強を進めるポイントと未習分野の勉強方法

2023.03.20

ここで紹介している子は、「わからないところをできるようにするのが勉強」だとわかっているので、予習でも未知の問題でも全然抵抗なくササっと解き始めます。

ファイでは学年に関係なく受けたい授業を受けられるので、このような考えが自然と身に着いているのです。

ご家庭でも学年の枠を取り払って問題にあたってみるだけで同じことができます。

その子のレベルに合わせて適切に解釈をサポートしていく負担は確かにありますが、その価値は十分あります。

もしご家庭では難しいようなら、ファイで一緒に勉強してみませんか？

「わからないところをできるようにするのが勉強」という考えが自然と身に付けられますよ(^^)/