早稲田大学高等学院中の算数,面積の規則性を扱ったのでちょっとご紹介致します。
この問題は図形の角度さえ知っていれば解けますので,小4でも図形を扱っていれば解けるでしょう。
中学受験の勉強をしていない子なら小5かな。
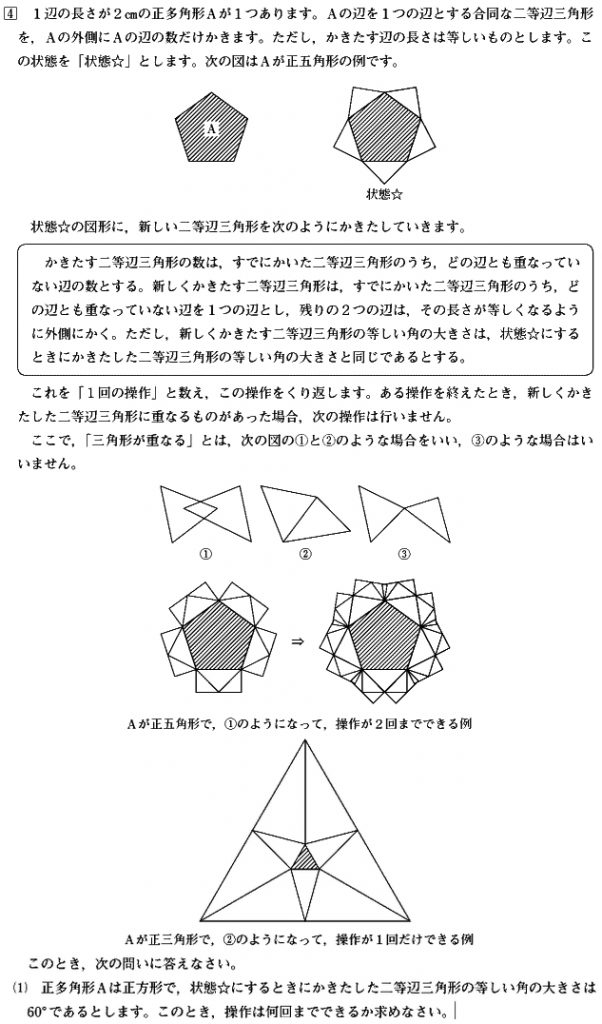
答え:2回まで
まずポイントとなるのは,問題文を正確に読み取る力があるかどうか。
ほとんどの子がここで挫折します。
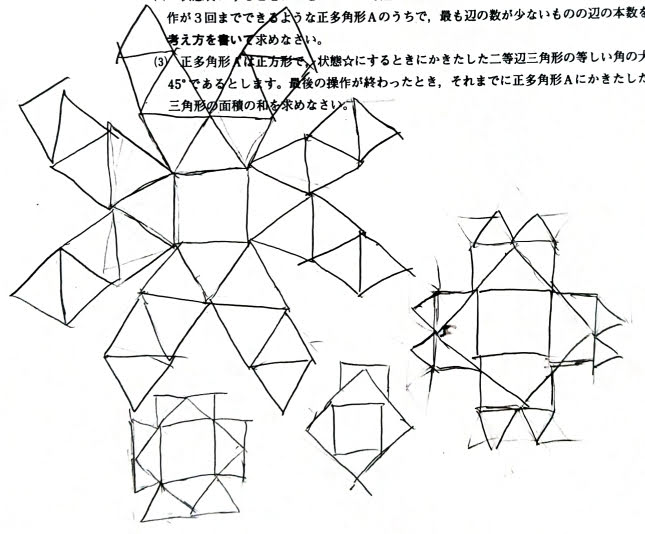
これはそもそも文章の意味が分かっていない子の典型例です。
重なったら終わりなのですが,重ならないように広げてしまっています。
こんな状態の子でも,問題の意味さえ正確に読み取れれば,この問題は大して難しい問題ではないのです。
端的に言うと,
真ん中の核となる図形の辺に,二等辺三角形をつける。その二等辺三角形の辺に,また二等辺三角形をつける。
ただこれを繰り返していって,重なってしまう,もしくは接してしまえばおしまい,というルールです。
なお,つけていく二等辺三角形は全て相似な図形(形は同じで大きさが違う図形)です。
ということです。
相似な二等辺三角形をくっつけていくだけなので,大きさは変わっても,増えていく角度は一緒というところに気付けるかがポイント。
例えば,底角が30度の二等辺三角形をつける場合,30度を2つで60度増える。
さらにその辺に同じ形の二等辺三角形をつけるので,また60度増える。
これの繰り返しで,重なるということは,360度以上になったらダメ,ということです。
(1)の問題の場合は,最初の核となる図形は正方形なので90度。
そこに正三角形をつけると60度×2で120度増える。
つまり90+120=210度
2回目をやるとまた120度増えるので,330度になる。
3回目をやると360度を超えるので,重なるということ。
よって2回までとわかります。
問題は,この手の問題にどう気付かせるか,ということ。
実は子どもはめんどくさがっているだけなことが多いので,ちょっと実際に書かせてあげればすぐに気づきます。
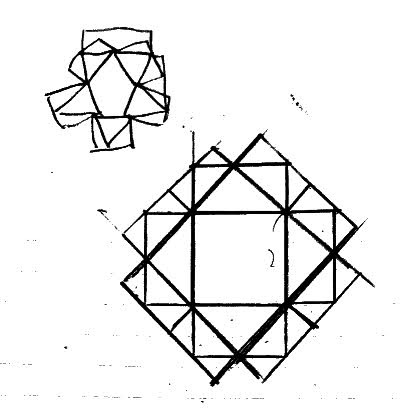
書いたり消したりをしているうちに気付いたため,プロセスとしてはこれだけしか残っていませんでした(^^;
しかしこのようにあれこれ書いていけば気付きやすくなります。
2辺だけ書いて解ければもっとスマートなのですが,その辺りはまだ気づきの詰めが甘い所ですね。

さて,(1)が解ければ(2)(3)もそんなに問題ではありません。
ここには問題を載せていませんが,この子たちも1が出来たらささっと全部解いてしまいました。
文章さえ読めれば小4でも解けるでしょうから,問題を読む力がどれだけあるかを試してみる指標になるでしょう。
もし問題を読む力が乏しい場合は,問題文に沿って,1つずつ自分で図形を書かせながら,文章の意味を理解していく練習をして下さい。
そんなに時間もかからず,理解の仕方をつかめるようになるでしょう。







-9-485x300.png)











コメントを残す