暗記と思考は、結論が一緒でも結果が異なる
他塾からファイに来た子はよくこのように言います。
聞くたびに、やはり受験のための教育は、知識の埋め込みに偏っているんだなと感じます。
知識として知っているのと、考えて理解するのとでは脳の使い方が大きく異なります。
それゆえ、同じ結論にたどり着いたものでも、それに至るまでにどのような過程を通って来たかで、知識としての使い方が大きく異なってくるのです。
例えばこのような問題はどうでしょうか。
暗記と思考の決定的な差
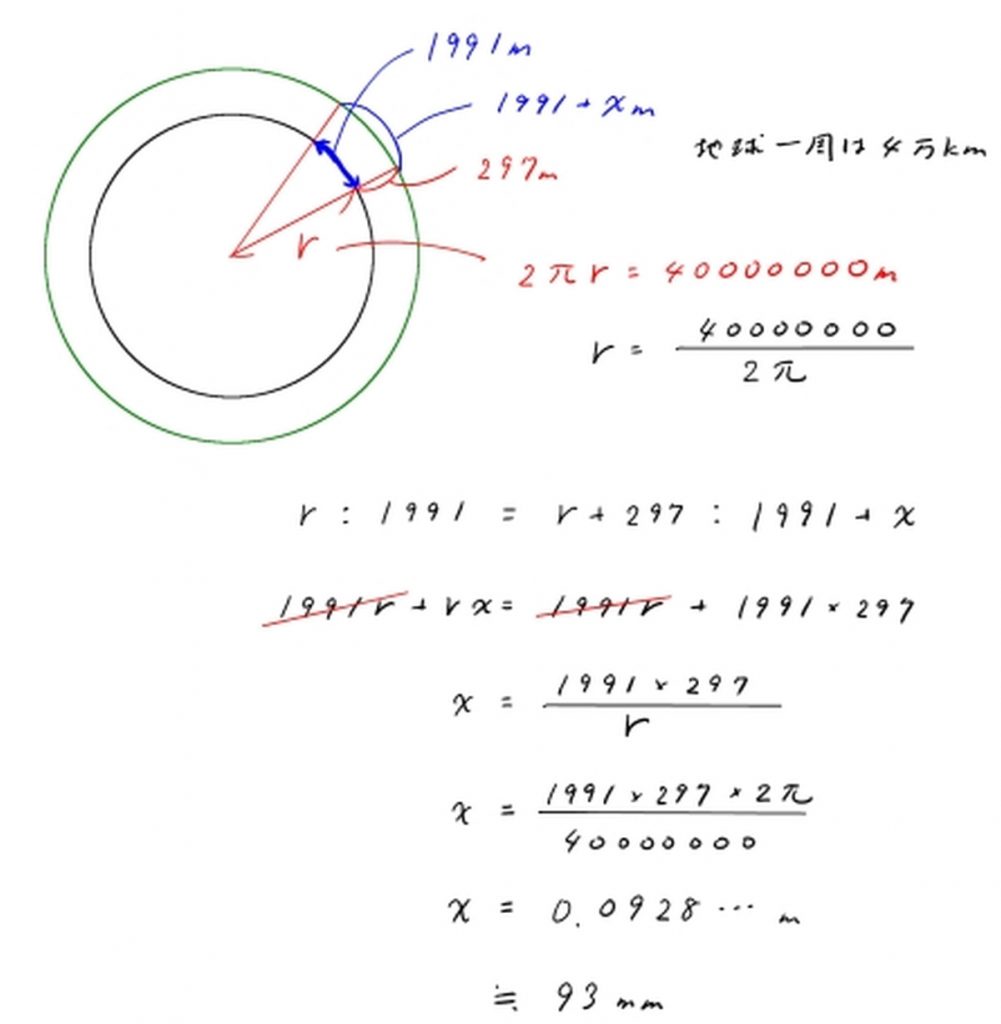
1998年に完成した当時世界一の吊橋、明石海峡大橋はケーブルを支えている2本の主塔の基部(根もと)の距離が1991m。ところが297m上にある塔のてっぺんでの距離は1991mと93mm。地面に垂直に立っているにも関わらず、上の方は93mmも開いてしまっている理由を説明しなさい。
誤差ではありません。
必然的にこうなるのです。
理由は地球が丸いから。
丸いボールに棒を立てれば、上に行くほど棒の間の距離が広くなっていく事がわかります。
これをこうやって教えられても「へー」となって、これで終わり。
これ以上発展させて考える子はほとんどいません。
しかしこれをこのように変えてみましょう。
「明石海峡大橋の主塔の基部の距離は1991m。297m上の塔の頂上の距離はどうなるか求めなさい。
このように聞くと、
「なんで?同じじゃないの?」
から始まり、子ども達は様々な事を考えます。
もちろん大半は迷走したような解答。
しかしその迷走の過程で平行線の概念、円の概念、円周の長さなどを理解し、最終的には長さを実際に求める子まで現れます。
こうして得た知識は、単に「地球が丸いから」ではありません。
地球の半径も知らなければならないと思いきや、地球の周りの長さが分かっていれば、半径を出すことができます。
そして地球一周の長さは1mの決め方を知っていれば大したことありません。
このように様々な視点から問題を考えられるようになり、それこそ算数ではなくても様々な視点から頭を使えるようになるのです。
すると知識量は最低限でも、答えを導ける頭の使い方ができるようになるのです。
ところでこの問題、実際に解くと大変そうに感じませんでしたか?
実はこの問題、大して難しくありません。
おうぎ形の弧の長さの求め方をわかっていれば、小学生でも解くことができます。
中学受験の特殊算も、高校受験のテクニックも必要ありません。
でも、覚えることを勉強だと思っている子は、問題を見た時点で苦痛に感じて解こうともしないのです。
これも大きな差を生みます。
大人はなにかと答えを教えたがりますが、子どもはそんな事望んでいないのです。
時間さえ許せば、子どもは自分で考えている時間の方が楽しいのです。
ま、時間がないから詰め込み教育の塾がはやるんですけどね(^^;
従来の詰め込み教育に限界を感じているなら、ファイにご連絡下さい。
子供の些細な疑問には、学び方のチャンスが沢山転がっています。
そんな子供の疑問から一緒に学んでいきましょう(^^)/








-9-485x300.png)




-6-485x300.png)







「今までこんなに何で?何で?って聞かれた事もなかったから、考えた事もなかった。今まで勉強は暗記するものだと思ってた。」